このページはまだ翻訳されていません。原文の内容が表示されています。
path要素関数要素関数要素関数はsetルールやshowルールでカスタマイズできます。
setルールやshowルールでカスタマイズできます。A path through a list of points, connected by Bézier curves.
Example
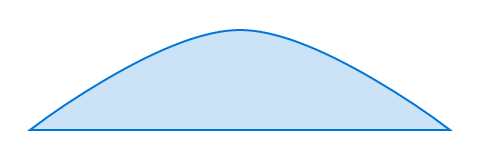
#path(
fill: blue.lighten(80%),
stroke: blue,
closed: true,
(0pt, 50pt),
(100%, 50pt),
((50%, 0pt), (40pt, 0pt)),
)
引数引数引数は関数への入力値です。関数名の後に括弧で囲んで指定します。
fill
How to fill the path.
When setting a fill, the default stroke disappears. To create a rectangle with both fill and stroke, you have to configure both.
デフォルト値: none
fill-rule設定可能引数設定可能引数設定可能引数は、setルールを用いて設定でき、それ以降で使用するデフォルト値を変更できます。
setルールを用いて設定でき、それ以降で使用するデフォルト値を変更できます。The drawing rule used to fill the path.
使用可能な文字列値:
non-zeroSpecifies that "inside" is computed by a non-zero sum of signed edge crossings.
even-oddSpecifies that "inside" is computed by an odd number of edge crossings.
デフォルト値: "non-zero"
例を表示
// We use `.with` to get a new
// function that has the common
// arguments pre-applied.
#let star = path.with(
fill: red,
closed: true,
(25pt, 0pt),
(10pt, 50pt),
(50pt, 20pt),
(0pt, 20pt),
(40pt, 50pt),
)
#star(fill-rule: "non-zero")
#star(fill-rule: "even-odd")

stroke
How to stroke the path. This can be:
Can be set to none to disable the stroke or to auto for a
stroke of 1pt black if and if only if no fill is given.
デフォルト値: auto
closed設定可能引数設定可能引数設定可能引数は、setルールを用いて設定でき、それ以降で使用するデフォルト値を変更できます。
setルールを用いて設定でき、それ以降で使用するデフォルト値を変更できます。Whether to close this path with one last Bézier curve. This curve will take into account the adjacent control points. If you want to close with a straight line, simply add one last point that's the same as the start point.
デフォルト値: false
vertices必須引数必須引数必須引数は、関数を呼び出す際に必ず指定しなければなりません。位置引数位置引数位置引数は順序通りに指定することで、引数名を省略して設定できます。可変長引数可変長引数可変長引数は複数回指定することができます。
The vertices of the path.
Each vertex can be defined in 3 ways:
- A regular point, as given to the
lineorpolygonfunction. - An array of two points, the first being the vertex and the second being the control point. The control point is expressed relative to the vertex and is mirrored to get the second control point. The given control point is the one that affects the curve coming into this vertex (even for the first point). The mirrored control point affects the curve going out of this vertex.
- An array of three points, the first being the vertex and the next being the control points (control point for curves coming in and out, respectively).